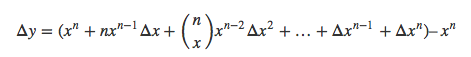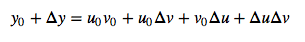The Derivative Toolbox

The method for taking a derivative depends on the type of function you want to find the derivative of. There are a set of rules that address the possible ways you can take the derivative, and we will call this set of rules the derivative toolbox. We’ve already touched on one, and that is the power rule. Let’s suppose we want to take the derivative of some function $x^{n}$ .

$f(x) = x^{n}$ .

What is the derivative of this function?

$f'(x) = \frac{dy}{dx}(x^{n})$

Well, let’s apply the method of increments and see if we can make some sense of this.

$\Delta y = (x + \Delta x)^{n} - (x^{n})$

Let’s expand this expression… We can use the binomial expansion!

The first and the last term are going to cancel, leaving us with…

Now, if we divide by $\Delta x$ and observe the function as $\lim \limits_{\Delta x \to 0}$ .

$\lim \limits_{\Delta x \to 0}\frac{\Delta y}{\Delta x } = \frac{nx^{n-1}\Delta x + \binom{n}{x}x^{n-2}\Delta x^{2} + ... + x\Delta x^{n-1} + \Delta x^{n}}{\Delta x}$

The $\Delta x$ in the first term will cancel out, and the rest of the terms will go to zero, leaving us with…

$\lim \limits_{\Delta x \to 0}\frac{\Delta y}{\Delta x } = nx^{n-1}$

Or, alternatively…

$f'(x) = nx^{n-1}$

Boom! There we have it, the power rule! This rule works for any function of the form $x^{n}$

There are two other fundamental rules for differential calculus, the product rule and the chain rule.

Let’s start with the product rule. What do you do if you want to take the derivative of the function:

$y = (x^{2} + 3)x^{3}$

There are two possible strategies, first let’s take the derivative of the components and then multiply them together.

$y' = (2x)3x^{2} = 6x^3$

The second is that we could multiply through by the cubed term.

$y = x^{5} + 3x^{3}$

$y' = 5x^{4} + 9x^{2}$

These two methods don’t agree! Which one is correct? Let’s use the method of increments. Pretend our two expressions above are variables, u and v.

$y = uv$

Both u and v are functions of x, so at $x = x_{0}$ , the variables have the values:

$y_{0} = u_{0}v_{0}$

This is probably getting old by now, but let’s increment by $\Delta x$

$y_{0} + \Delta y = (u_{0} + \Delta u)(v_{0} + \Delta v)$

Expanding this out gives

Simplifying by substituting our y-values in gives

The average rate of change of y with respect to x in the interval of $\Delta x$ is obtained by dividing by $\Delta x$ and taking the limit as $\Delta x$ goes to 0.

The following simplifies to

This is the product rule! Are you scratching your head and asking how the big expression above simplify to this diminuitive expression? Well, we have firmly established that the derivative is the limit of the change of y divided by the change of x as the change in x goes to 0. The terms $(\frac{\Delta v}{\Delta x}) , (\frac{\Delta u}{\Delta x})$ in the expression above simplify to $v'$ and $u'$ , the derivatives of these two expressions. The third term goes to 0, because the change in u is very very close to 0.